Introduction

Heron’s formula is an important concept in geometry, specifically for calculating the area of a triangle when the lengths of all three sides are known. It is named after Hero of Alexandria, an ancient Greek mathematician. This formula provides a method to determine the area of any triangle without needing the height or altitude of the triangle, making it a valuable tool in geometry and trigonometry.

In this chapter, we will explore Heron’s formula, its derivation, and its application in solving various types of problems related to triangles.

The Formula

The area A of a triangle with sides a, b, and c is given by the following formula:

Where:

• a, b, and c are the lengths of the sides of the triangle.
• s is the semi-perimeter of the triangle, which is calculated as:

Understanding Heron’s Formula

Step 1: Semi-perimeter (s)

The first step in using Heron’s formula is to find the semi-perimeter sss. The semi-perimeter is half the perimeter of the triangle. If the perimeter P is the sum of the lengths of all three sides, then the semi-perimeter is simply:

For example, if a triangle has side lengths a=5, b=6, and c=7, then:

Step 2: Applying Heron’s Formula

Once you have the semi-perimeter, you can apply Heron’s formula to find the area. You substitute the values of a, b, and c into the formula and calculate the area.

For example, using the same values for a, b, and c, the area A is calculated as follows:

Thus, the area of the triangle is approximately 14.7 square units.

Derivation of Heron’s Formula

The derivation of Heron’s formula is a bit more complex, but it is essential to understand the reasoning behind the formula. The formula is derived from the general expression for the area of a triangle using its base and height.

Let’s consider a triangle with sides a, b, and c, where the height h is perpendicular to the base b.

Area of Triangle Using Base and Height: The area A of the triangle can be expressed as:

For our triangle, if we choose b as the base, the area becomes:

Using Pythagoras Theorem: If we draw an altitude from the vertex opposite the base, it divides the triangle into two right-angled triangles. We can apply the Pythagorean theorem to calculate the height in terms of the sides a, b, and c.

After a series of algebraic manipulations involving the Pythagorean theorem and the law of cosines, we arrive at Heron’s formula, which avoids the need to know the height explicitly.

Examples of Using Heron’s Formula

Example 1:

Find the area of a triangle whose sides are 7 cm, 8 cm, and 9 cm.

Solution:

1. Calculate the semi-perimeter s:

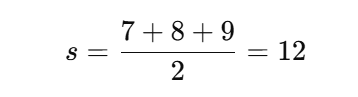
2. Substitute the values into Heron’s formula:

Thus, the area of the triangle is approximately 26.83 square centimeters.

Example 2:

A triangle has sides of lengths 12 cm, 13 cm, and 15 cm. Find its area.

Solution:

1. First, calculate the semi-perimeter s:

2. Now, apply Heron’s formula:

Thus, the area of the triangle is approximately 74.83 square centimeters.

Applications of Heron’s Formula

1. Solving for Area with Known Side Lengths: The most direct use of Heron’s formula is to calculate the area of a triangle when the lengths of all three sides are known.
2. Irregular Triangles: Heron’s formula is especially useful for calculating the area of irregular triangles, where the altitude or height is not easily known or difficult to measure. In these cases, knowing the side lengths is sufficient.
3. Geometric Problems Involving Triangles: Heron’s formula is frequently used in geometry problems where triangles are formed by intersecting lines, and the area needs to be calculated.
4. Applications in Real-World Geometry: This formula has practical applications in fields such as architecture, engineering, and physics, where precise area calculations of triangular shapes are required.

Properties of Heron’s Formula

• Simplicity: Heron’s formula allows the calculation of the area without the need for the height, which can be difficult to measure in many situations.
• Universality: Heron’s formula works for all types of triangles, including acute, obtuse, and right-angled triangles.
• Flexibility: The formula is especially useful in problems involving multiple triangles with known side lengths.

Conclusion

Heron’s formula is a powerful tool in geometry, enabling the calculation of the area of a triangle from its side lengths. Understanding and applying Heron’s formula is crucial for solving various geometric problems in mathematics, especially in cases where the altitude is unknown. By mastering Heron’s formula, students can easily tackle complex geometric problems and gain a deeper understanding of the properties of triangles.

It is important to note that Heron’s formula is only applicable to triangles, so it’s crucial to ensure that the given lengths form a valid triangle (i.e., the sum of any two sides should be greater than the third side).