Metrices class 12 is an array of numbers. In other words, it is an arrangement of numbers into rows and columns.
A matrix A of order 3×3 can be represented as:

Equality of Matrices
For matrices to be equal. It is best to consider that:
- The order of matrices should be the same.
- All the elements should be the same.
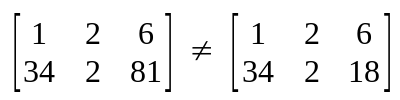
Important Formulas for Matrices
- (a) A (adj.A) = | A | in = (adj A) A
- (b) | adj A | = | A |n-1 (Thus A (adj A) is always a scalar matrix)
- (c) Adj (adj.A) = | A |n-2 A
- (d) Adj (AB) = (adj B) (adj A)
- (e) Adj (Am) = (adj A) m,
- (f) A is symmetric ⇒adj A is also symmetric
- (g) Adj 0 = 0
- (h) A is symmetric ⇒adj A is also symmetric
- (i) A is diagonal ⇒adj A is also diagonal
- (j) A is triangular ⇒adj A is also triangular
- (k) A is singular ⇒| adj A | = 0
- (i) Symmetric Matrix: A square matrix A = [aij] is called a symmetric matrix if aij = aji.
- (ii) Skew-Symmetric Matrix: when aij = -aji
Types of Matrices
Other Types of Metrices
Matrices class 12 is one of the most important chapters of mathematics, which helps you obtain good marks in board exams and is also beneficial in higher studies. Given below are some of the types of matrices:
Column Metrices
Column metrices mean the matrix consists of only one column. For example, A = [aij] m × 1 is a column matrix of order m × 1.
Row Metrices
You can call it a Row matrix when it consists of only one row. When we see, A = [aij] 1 × n is a column matrix of order 1 x n.
Square Metrices
Square metrices are defined as the matrix in which the rows and columns appear to be equally the same. In general, the m × n matrix is called square matrix only if m = n and is known as the square matrix of order ‘n.’ Suppose, A = [aij] n x n is a square matrix of order n.
Diagonal Metrices
A square matrix B = [bij] m × m is a diagonal matrix if all its non-diagonal elements are zero. That is matrix B = [bij] m × m is said to be a diagonal matrix if bij = 0, when i ≠ j.
Identity Metrices
Identity matrices are defined as the square matrix where all the components in the diagonal are valued one and the rest components are valued zero.
For example, in denotes, the identity matrix N. Suppose the scalar matrix is the identity matrix when K=1.
Zero Metrices
Those matrices are said to be the zero matrix whose all the components are valued at zero. O denotes zero matrices.